Generalita' sul Formalismo dei Quadri-Vettore
nello Studio delle Reazioni Nucleari
Per prima cosa si consideri un sistema di riferimento (SR) inerziale solidale con le stelle fisse. In tale "SR" il tempo sara' misurato con orologi normali e la posizione di un evento E verra' descritta in termini delle coordinate cartesiane del "punto" in questione. In tale SR supponiamo di utilizzare il sistema "c1", ovvero si scelga come unita' di misura della velocita' la velocita' della luce nel vuoto e si ponga c=1. In tal modo la velocita' sara' una grandezza adimensionale. Con tale assunzione le quantita' energia E, massa M, quantita' di moto P avranno tutte le stesse dimensioni che per comodita' supponiamo sia il Mev.
Un evento E sara' descritto da una posizione x e da un istante di tempo t. E' possibile ora associare all' evento in questione la quantita' seguente:
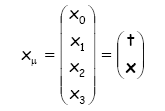
nota come 4-vettore, dove la quantita' x puo' anche variare nel tempo. Per quanto concerne il 4-vettore velocita', senza entrare nel dettaglio per la sua determinazione, si puo' affermare che esso e' dato dalla seguente quantita':
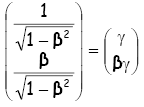
In quadri-momento e' invece dato da:
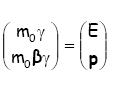
Sono, inoltre, particolarmente utili le seguenti quantita':
che mostra il legame tra l' energia totale della particella di massa mo ed il relativo impulso o quantita' di moto,
che in pratica e' la formula inversa della precedente,
che mostra il legame tra l' energia totale E e l' energia cinetica della particella di massa mo,
che mostra il legame tra la quantita' di moto di una particella di massa mo con la sua energia cinetica T.
I quadrivettori, godono di talune proprieta' matematiche assai utili ed interessanti quali:
LA SOMMA DI DUE 4-VETTORI E' DEFINITA NEL MODO SEGUENTE:
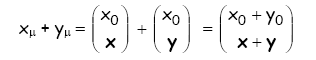
IL PRODOTTO SCALARE TRA DUE 4-VETTORI E' DEFINITO NEL MODO SEGUENTE:
IL MODULO QUADRO DI UN 4-VETTORE E' DATO DALLA SEGUENTE RELAZIONE:
IL MODULO DEI 4-VETTORE E' UN INVARIANTE RELATIVISTICO.
Nel caso di una reazione nucleare del tipo:
utilizzando il formalismo dei 4-vettori su accennato, si ha la conservazione del 4-momento che sintetizza la conservazione dell' energia e della quantita' di moto, ovvero:
indicando, ora, con "1" la particella
incidente, con "2" il bersaglio, con "3" e "4"
i prodotti della reazione il calcolo del momento p3
oppure E3 della particella "3" in funzione della
sua direzione di volo indicato dall' angolo che essa forma con la direzione
iniziale della particella "1" ed indicata con 
e'
dato dalla seguente relazione:
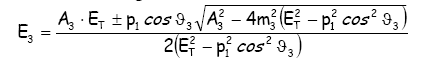
dove
per quanto concerne l' energia del prodotto
della reazione "4" e relativa direzione di volo 
si
ha:
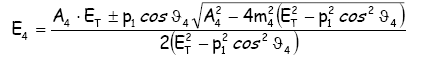
dove
Si osservi che la condizione che il radicando,
nelle espressioni precedenti, risulti >= 0 fissa un limite
per gli angoli e
,
ovvero determina un limite alle direzioni di volo delle particelli uscenti
della reazione nucleare "3" e "4". Quantitativamente si
ottiene:
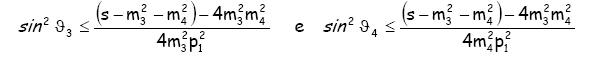
Si osservi che ponendo
oppure
= 0, dalle relazioni precedenti e' possibile ottenere il valore dell' Energia
cinetica di soglia della reazione nucleare. Si rammenta che
quest' ultima quantita' indica il minimo valore dell' Energia Cinetica
T della particella "1" (il "proiettile") che rende possibile
la reazione nucleare. Un' espressione esplicita di tale quantita'
vale:
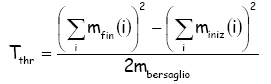
oppure
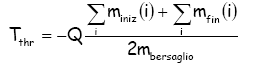
In quest' ultima relazione Q indica il cosiddetto Q-value della reazione che vale:
ed il cui valore indica la "fattibilita'" o meno della reazione nucleare in questione; Q > 0 reazione esotermica ovvero reazione che avviene spontaneamente anche con energia cinetica nulla del proiettile.
Ritornando alle equazioni per
oppure
si osservi che se le relazioni a secondo membro risultano < 1,
vi e' l' esistenza di un angolo limite 
.
In tal caso, l' intervallo di valori dell' angolo delle direzioni di volo
per la particella emessa vale:
Se invece le relazioni a secondo membro risultano > 1, non esiste per la particella in questione alcun angolo limite e puo', pertanto, essere emessa nell' intervallo:
