Operators and Quantum Mechanics

Next: Basic Properties of Operators Up: Operators Previous: Operators

Operators and Quantum Mechanics

In quantum mechanics, physical observables (e.g., energy, momentum, position, etc.) are represented mathematically by operators. For instance, the operator corresponding to energy is the Hamiltonian operator

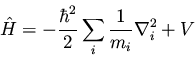$\begin{displaymath}\hat{H} = - \frac{\hbar^2}{2} \sum_i \frac{1}{m_i} \nabla_i^2 + V \end{displaymath}$

(31)

where i is an index over all the particles of the system. We have already encountered the single-particle Hamiltonian in equation (25). The average value of an observable A represented by an operator $\hat{A}$ for a quantum molecular state $\psi({\bf r})$ is given by the ``expectation value'' formula

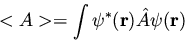$\begin{displaymath}<A> = \int \psi^{*}({\bf r}) \hat{A} \psi({\bf r}) \end{displaymath}$

(32)