next up previous contents
Next: Commutators in Quantum Mechanics Up: Operators Previous: Hermitian Operators

Unitary Operators

A linear operator whose inverse is its adjoint is called unitary. These operators can be thought of as generalizations of complex numbers whose absolue value is 1.
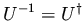$\displaystyle U^{-1} = U^{\dagger}$     (63)
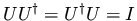$\displaystyle U U^{\dagger} = U^{\dagger} U = I$      

A unitary operator preserves the ``lengths'' and ``angles'' between vectors, and it can be considered as a type of rotation operator in abstract vector space. Like Hermitian operators, the eigenvectors of a unitary matrix are orthogonal. However, its eigenvalues are not necessarily real.