Commutators in Quantum Mechanics

Next: Linear Vector Spaces in Up: Mathematical Background Previous: Unitary Operators

Commutators in Quantum Mechanics

The commutator, defined in section 3.1.2, is very important in quantum mechanics. Since a definite value of observable A can be assigned to a system only if the system is in an eigenstate of $\hat{A}$ , then we can simultaneously assign definite values to two observables A and B only if the system is in an eigenstate of both $\hat{A}$ and $\hat{B}$ . Suppose the system has a value of A_i for observable A and B_j for observable B. The we require

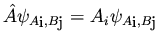$\displaystyle \hat{A} \psi_{A_i,B_j} = A_i \psi_{A_i,B_j}$			(64)
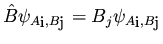$\displaystyle \hat{B} \psi_{A_i,B_j} = B_j \psi_{A_i,B_j}$

If we multiply the first equation by $\hat{B}$ and the second by $\hat{A}$ then we obtain

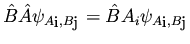$\displaystyle \hat{B} \hat{A} \psi_{A_i,B_j} = \hat{B} A_i \psi_{A_i,B_j}$			(65)
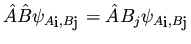$\displaystyle \hat{A} \hat{B} \psi_{A_i,B_j} = \hat{A} B_j \psi_{A_i,B_j}$

and, using the fact that $\psi_{A_i,B_j}$ is an eigenfunction of $\hat{A}$ and $\hat{B}$ , this becomes

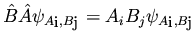$\displaystyle \hat{B} \hat{A} \psi_{A_i,B_j} = A_i B_j \psi_{A_i,B_j}$			(66)
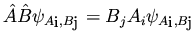$\displaystyle \hat{A} \hat{B} \psi_{A_i,B_j} = B_j A_i \psi_{A_i,B_j}$

so that if we subtract the first equation from the second, we obtain

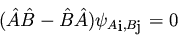$\begin{displaymath}(\hat{A} \hat{B} - \hat{B} \hat{A}) \psi_{A_i,B_j} = 0 \end{displaymath}$

(67)

For this to hold for general eigenfunctions, we must have $\hat{A} \hat{B} = \hat{B} \hat{A}$ , or $[\hat{A}, \hat{B}] = 0$ . That is, for two physical quantities to be simultaneously observable, their operator representations must commute.

Section 8.8 of Merzbacher [2] contains some useful rules for evaluating commutators. They are summarized below.

$\begin{displaymath}[ {\hat A}, {\hat B} ]+ [ {\hat B}, {\hat A} ] = 0 \end{displaymath}$

(68)

$\begin{displaymath}[ {\hat A} , {\hat A} ]= 0 \end{displaymath}$

(69)

$\begin{displaymath}[ \hat{A}, \hat{B} + \hat{C} ]= [ \hat{A}, \hat{B} ] + [ \hat{A}, \hat{C} ] \end{displaymath}$

(70)

$\begin{displaymath}[ \hat{A} + \hat{B}, \hat{C} ]= [ \hat{A}, \hat{C} ] + [ \hat{B}, \hat{C} ] \end{displaymath}$

(71)

$\begin{displaymath}[ \hat{A}, \hat{B} \hat{C} ]= [ \hat{A}, \hat{B} ] \hat{C} + \hat{B} [\hat{A}, \hat{C} ] \end{displaymath}$

(72)

$\begin{displaymath}[ \hat{A} \hat{B}, \hat{C} ]= [ \hat{A}, \hat{C} ] \hat{B} + \hat{A} [\hat{B}, \hat{C} ] \end{displaymath}$

(73)

$\begin{displaymath}[ \hat{A}, [ \hat{B}, \hat{C} ]] + [\hat{C}, [ \hat{A}, \hat{B}] ] + [ \hat{B}, [ \hat{C}, \hat{A}] ] = 0 \end{displaymath}$

(74)

If $\hat{A}$ and $\hat{B}$ are two operators which commute with their commutator, then

$\begin{displaymath}[\hat{A}, \hat{B}^{n}]= n \hat{B}^{n-1} [\hat{A}, \hat{B}] \end{displaymath}$

(75)

$\begin{displaymath}[\hat{A}^{n}, \hat{B}]= n \hat{A}^{n-1} [\hat{A}, \hat{B}] \end{displaymath}$

(76)

We also have the identity (useful for coupled-cluster theory)

$\begin{displaymath}e^{\hat{A}} \hat{B} e^{-\hat{A}} = \hat{B} + [\hat{A},\hat{B}... ...{1}{3!} [ \hat{A}, [ \hat{A}, [ \hat{A}, \hat{B}] ] ] + \cdots \end{displaymath}$

(77)

Finally, if $[ \hat{A}, \hat{B} ] = i \hat{C}$ then the uncertainties in A and B, defined as $\Delta A = <A^2> - <A>^2$ , obey the relation¹

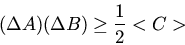$\begin{displaymath}(\Delta A) (\Delta B) \geq \frac{1}{2} <C> \end{displaymath}$

(78)

This is the famous Heisenberg uncertainty principle. It is easy to derive the well-known relation

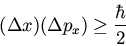$\begin{displaymath}(\Delta x) (\Delta p_x) \geq \frac{\hbar}{2} \end{displaymath}$

(79)

from this generalized rule.

Next: Linear Vector Spaces in Up: Mathematical Background Previous: Unitary Operators