The Harmonic Oscillator

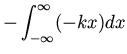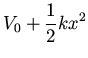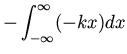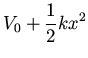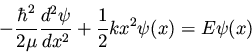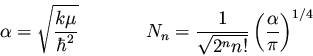
Next: The Rigid Rotor Up: Some Analytically Soluble Problems Previous: The Particle in a

The Harmonic Oscillator

Now consider a particle subject to a restoring force F = -kx, as might arise for a mass-spring system obeying Hooke's Law. The potential is then

V(x)	=	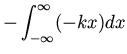$\displaystyle - \int_{-\infty}^{\infty} (-kx) dx$	(118)
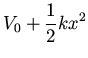	=	$\displaystyle V_0 + \frac{1}{2} kx^2$

If we choose the energy scale such that V₀ = 0 then V(x) = (1/2)kx². This potential is also appropriate for describing the interaction of two masses connected by an ideal spring. In this case, we let x be the distance between the masses, and for the mass m we substitute the reduced mass $\mu$ . Thus the harmonic oscillator is the simplest model for the vibrational motion of the atoms in a diatomic molecule, if we consider the two atoms as point masses and the bond between them as a spring. The one-dimensional Schrödinger equation becomes

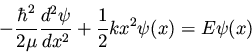$\begin{displaymath}- \frac{\hbar^2}{2 \mu} \frac{d^2\psi}{dx^2} + \frac{1}{2} kx^2 \psi(x) = E \psi(x) \end{displaymath}$

(119)

After some effort, the eigenfunctions are

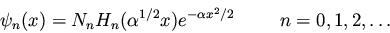$\begin{displaymath}\psi_n(x) = N_n H_n(\alpha^{1/2} x) e^{-\alpha x^2 / 2} \hspace{1.0cm} n=0,1,2,\ldots \end{displaymath}$

(120)

where H_n is the Hermite polynomial of degree n, and $\alpha$ and N_n are defined by

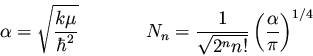$\begin{displaymath}\alpha = \sqrt{\frac{k \mu}{\hbar^2}} \hspace{1.5cm} N_n = \frac{1}{\sqrt{2^n n!}} \left( \frac{\alpha}{\pi} \right)^{1/4} \end{displaymath}$

(121)

The eigenvalues are

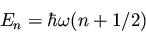$\begin{displaymath}E_n = \hbar \omega (n + 1/2) \end{displaymath}$

(122)

with $\omega = \sqrt{k/ \mu}$ .

Next: The Rigid Rotor Up: Some Analytically Soluble Problems Previous: The Particle in a