The Rigid Rotor

Next: The Hydrogen Atom Up: Some Analytically Soluble Problems Previous: The Harmonic Oscillator

The Rigid Rotor

The rigid rotor is a simple model of a rotating diatomic molecule. We consider the diatomic to consist of two point masses at a fixed internuclear distance. We then reduce the model to a one-dimensional system by considering the rigid rotor to have one mass fixed at the origin, which is orbited by the reduced mass $\mu$ , at a distance r. The Schrödinger equation is (cf. McQuarrie [1], section 6.4 for a clear explanation)

$\begin{displaymath}- \frac{\hbar^2}{2I} \left[ \frac{1}{sin \theta} \frac{\par... ...\frac{\partial^2}{\partial \phi^2} \right] \psi(r) = E \psi(r) \end{displaymath}$

(123)

After a little effort, the eigenfunctions can be shown to be the spherical harmonics $Y_J^M(\theta, \phi)$ , defined by

$\begin{displaymath}Y_J^M(\theta, \phi) = \left[ \frac{(2J + 1)}{4 \pi} \frac{(... ...)!} \right]^{1/2} P_J^{\vert M\vert}(cos \theta) e^{iM \phi} \end{displaymath}$

(124)

where P_J^|M|(x) are the associated Legendre functions. The eigenvalues are simply

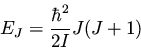$\begin{displaymath}E_J = \frac{\hbar^2}{2I} J(J+1) \end{displaymath}$

(125)

Each energy level E_J is 2J+1-fold degenerate in M, since M can have values $-J, -J+1, \ldots, J-1, J$ .